从电路到计算机
计算机和其它机器一样,不管它看起来有多复杂,都是从相当简单的东西一步一脚印地建成的。现在我们由普通中学生能理解的普通物理常识出发,说明计算机的关键组件可以如何实现。当然,商用的计算机集结了许多能干工程师的智慧来进行了高度优化,不像我们粗陋的原型,但产品正是从原型变出来的。
逻辑元件
首先回顾常用的逻辑电路组件,由名字应该可猜到它们的真值表:
| 逻辑元件 | 记号 |
|---|---|
| 中继器 | 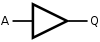 |
| NOT门 | 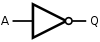 |
| AND门 | 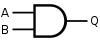 |
| NAND门 |  |
| OR门 | 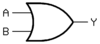 |
| NOR门 | 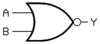 |
| XNOR门 | 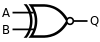 |
| XOR门 | 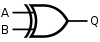 |
在离散数学中大家证过NAND单独就是完备的联结词组,所以我会只用说明如何实现NAND门,然后其它门也就能实现。
实现NAND门的方法不只一种,不过以下是明显的实现方法,用到两个电子开关(高平时开关断开),不过实际上用MOS管更靠谱一点。
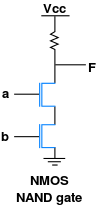
由于电子开关大家在初等的物理课都学过,这里不再深究其更底层的实现。
运算器
接下来我们看如何实现整数加法,简单地说就是复习小学的内容。标准算加法从最低位开始一位一位地做:每次把对齐的两个位连同前一步进位加起来,得到结果的一位和新的进位。为简化见还不如化为两次单位相加,这步骤需要两位输出和两位输出,实现是简单的,把它叫半加器:
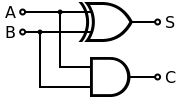
现在容易实现3位相加,只需要两个半加器,把它叫全加器:
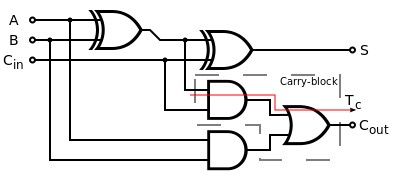
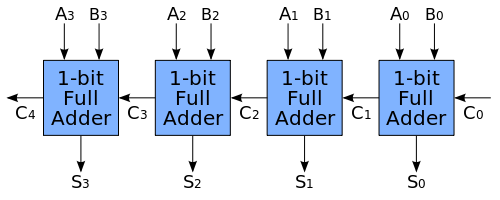
为方便见以后把全加器记为:

借助于封装的威力,我们现在可以简洁地给出给出整数加法的实现:
当然,我们同样会实现减法和乘法等算术运算了。这些实现的性能也许远非最优,工程师为此用了很大的努力来优化,但我们先不多说以防离题。
控制器
仅有运算器还不够,我们还要控制器以实现跳转,只能通过接电路来操作的计算机不能说是完整的。
可编程性(冯诺依曼架构的核心思想)的关键在于把控制表达为数据,这就需要可以按数据决定控制流。更具体地,就是用二进制数(一位对应一条输入线路)为输入,让对应于该序号的输出线路出真,这就是所谓的译码器。
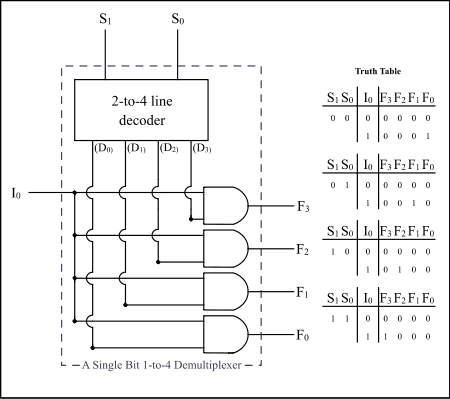
利用析取范式总可以设计出这样的电路虽然可能用的元件不是最少的。
反过来也可以想到有用途相反的编码器,用编码器和译码器就可以多路复用,多路复用实际上是制造控制器的基本手段。
存储器
我们还需要存储单元,这种电路不仅与电路的输入有关,而且与电路的前一状态有关,所以把这样的电路称为时序电路,而前述的简单电路称为组合电路。
为了做到这个效果,自然想到把输出线路反过来接到某输入线路。
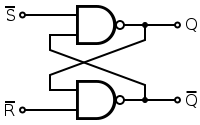
上面的SR锁存器在输入S和R均为1时输出Q会一直保持,在S和R分别为0和1(1和0)时,输出Q被设为1(0)。为了更接近使用逻辑和消除不稳定态,常把SR锁存器包装为D锁存器。
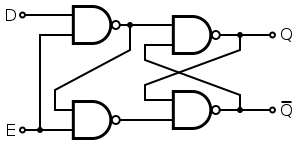
置位信号为0时输出保持,而置位信号为0时输出改为输入D。既然一个D锁存器可以保存一位,一组D锁存器就可以保存一组位,于是我们可以实现寄存器,与译码器相结合就可造可寻址的内存。
通常各个置位信号都来自同一时钟,它定时地发出脉冲以进行同步。
诺依曼体系计算机
至此,我们已经能够制作完整的诺依曼体系计算机,包括运算器、控制器和存储器,输入/输出设备原理也无异。LC-3是Patt在《计算机系统概论》中给出的一个例子:
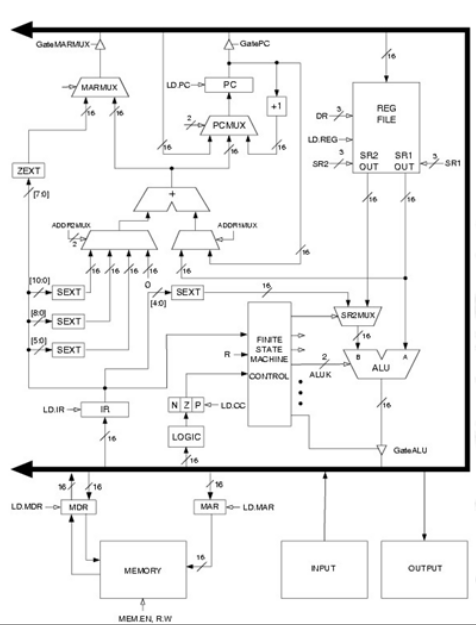
它虽然有点粗糙的,但原则上无疑能完成任何其它诺依曼体系计算机能做的事。
回顾我们激动人心的旅程,最关键的一点经验在于,抽象就是全部工程的基础,学会忘却才能看得更远。抽象并不抽象,只不过是用具体的东西搭建具体的东西,由此控制认知复杂度。
谁发明了计算机?
是数学家吗?数学至多是众多辅助工具之一,巴贝奇和图灵之类的人对实际计算机的设计假如不是零影响的话也远不如更早的可编程织布机,完全不需要他们,可见数学家连争功的资格都没有。
是物理学家吗?计算机的制造虽然用了一些物理原理,但用到的基本上都是早已众所周知的,问题只在于把它们组合起来,可见物理学决不是制约因素。
现在答案很清晰,在计算机的发明和后续发展中,电子工程师才是居功至伟的。他们越不被宣扬,他们的影响就越扎实、深刻、广泛而持久。仅以此文向这些沉默的实干家致敬。